

|
方程与曲线 |
概念 |
在平面直角坐标系中,如果某曲线C上的点的坐标(x,y)都是方程F(x,y)=0的解;反之方程F(x,y)=0的解为坐标的点(x,y)都在曲线C上,那么方程F(x,y)=0叫曲线C的方程,曲线C叫方程F(x,y)=0的曲线。 |
| 已知曲线求它的方程的步骤 | (1)建立适当坐标系,用(x,y)表示曲线上任一点P的坐标;
(2)写出适合条件M的点P的集合 (3)用坐标表示条件M(P),列出方程;f(x,y)=0 (4)化方程f(x,y)=0为最简形式 (5)证明化简后的方程的解为坐标的点都是曲线上的点 | |
| 充分条件 | 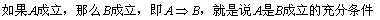 |
|
| 必要条件 |  |
|
| 充要条件 |  |
|